本文整理了神经网络中batch normalization的相关知识。
1. Internal Covariate Shift问题
机器学习领域有个很重要的假设:独立同分布假设(IID, Independent and identically distributed),就是假设训练数据和测试数据是满足相同分布的,并且数据之间是独立的,这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。
Batch Normalization的论文标题为Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,是用来解决Internal Covariate Shift问题的。如果ML系统实例集合$(X,Y)$中的输入值$X$的分布老是变,这不符合IID假设,网络模型很难稳定的学规律。对于深度学习这种包含很多隐层的网络结构,在训练过程中,因为各层参数不停在变化,所以每个隐层都会面临covariate shift的问题,也就是在训练过程中,隐层的输入分布总是发生变化,这就是所谓的”Internal Covariate Shift”,Internal指的是深层网络的隐层,是发生在网络内部的事情,即covariate shift问题不只发生在输入层。
BatchNorm的基本思想是,让每个隐层节点的激活输入分布固定下来,这样就避免了Internal Covariate Shift问题了。这个思想受到之前的研究”白化“的启发,”白化“,就是对输入数据分布变换到0均值,单位方差的正态分布,这样神经网络会较快收敛。BN论文的作者认为,图像是深度神经网络的输入层,做白化能加快收敛,那么其实对于深度网络来说,其中某个隐层的神经元就是下一层的输入,意思是其实深度神经网络的每一个隐层都是输入层,不过是相对下一层来说而已,那么可以考虑对每个隐层都做白化。事实上,BN可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。
2. Batch Normalization的本质思想
因为深层神经网络在做非线性变换前的激活输入值随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值是大的负值或正值),所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。这也表明,BN层是用在激活函数之前的。
一句话概括:对于每个隐层神经元,把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布,使得非线性变换函数的输入值落入对输入比较敏感的区域,以此避免梯度消失问题。
3. Batch Normalization的公式
每个batch输入是$x = [x_0, x_1, \cdots, x_m]$,其中每个$x_i$都是一个样本, $m$ 是batch size。 假如在第一层后加入Batch Normalization layer后,$h_1$的计算就倍替换为下图所示的那样:
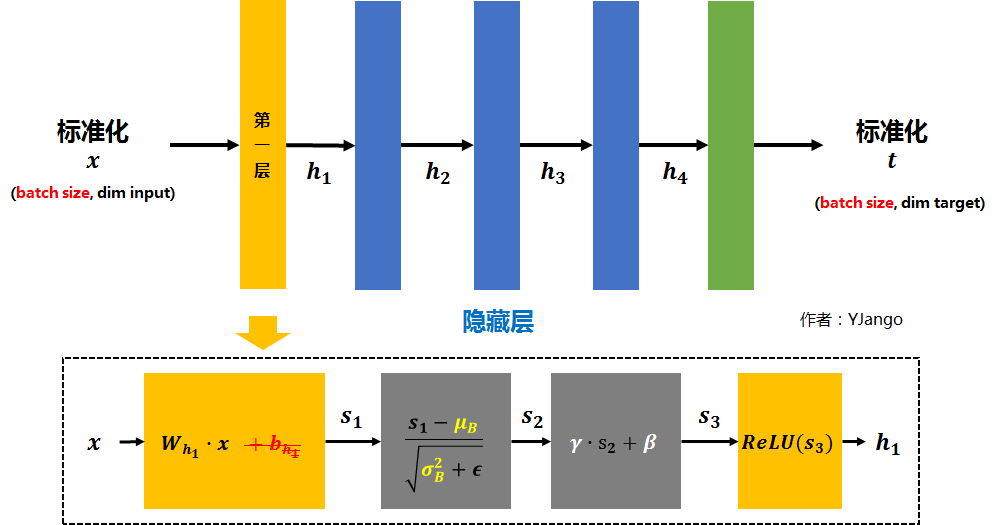
网络第一层的输入$x$到输出经过以下步骤:
$x$先经矩阵$W_{h_1}$线性变换得到$s_1$,因为后面减去batch的平均值$\mu_B$ 后,偏置$b_{h_1}$的作用会被抵消掉,所以没必要加入$b_{h_1}$(红色删除线)
对$s_1$做normalization,先减去当前batch的均值$\mu_B$,再除以标准差$\sqrt{\sigma_{B}^{2} + \epsilon}$,其中$\epsilon$是为了避免除数为0的情况所使用的微小正数,可以设置为$1 \times 10^{-7}$或$1 \times 10 ^ {-8}$
均值和标准差计算公式为:
- $\mu_B = \frac{1}{m} \sum_{i=1}^{m}s_{1i} = \frac{1}{m} \sum_{i=1}^{m}W_{h_1}x_i$
- $\sigma_{B}^{2} = \frac{1}{m}\sum_{i=1}^{m}(s_{1i} - \mu_B)^2$
这样得到$s_2 = \frac{s_1 - \mu_B}{\sqrt{\sigma_{B}^{2} + \epsilon}}$,现在$s_2$基本会被限制在均值为0,标准差为1的情况下,即符合正态分布,这会使得网络的表达能力下降
(为什么网络的表达能力下降了?因为如果网络层都用BN,就相当于把网络的非线性函数都用线性函数代替了,而多个线性层与一个线性层效果是等价的,这就降低了网络的非线性,使得网络的表达能力下降。)
所以BN为了保证非线性的获得,引入两个新的parameters:$\gamma$和$\beta$,这两个参数是网络自己学习得到的。通过scale和shift把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢
$\gamma$用于scale,$\beta$用于shift,$s_3 = \gamma \cdot s_2 + \beta$
最后加上激活函数
最后再加一张Batch Normalization论文里的算法流程:

4. Batch Normalization的推理(Inference)过程
需要注意的是,上述的计算方法用于在训练。因为测试时常会只预测一个新样本,也就是说batch size为1。若还用相同的方法计算$\mu_B$ ,$\mu_B$就会是这个新样本自身, $s_1 - \mu_B$就会成为0,所以在测试时,所使用的$\mu$和$\sigma^2$是整个训练集的均值$\mu_P$和方差$\sigma_P^2$,整个训练集的均值$\mu_P$和方差$\sigma_P^2$通常是在训练时用移动平均法来计算。
具体来说,每次做Mini-Batch训练时,都会有那个Mini-Batch里$m$个训练实例获得的均值$\mu_B$和方差$\sigma_B^2$,现在要全局统计量,只要把每个Mini-Batch的均值和方差统计量记住,然后对这些均值和方差求其对应的数学期望即可得出全局统计量,即
有了均值和方差,每个隐层神经元也已经有对应训练好的$\gamma$参数和$\beta$参数,就可以在推导的时候对每个神经元的激活数据计算NB进行变换了,在推理过程中进行BN采取如下方式:
写成这种形式,是在实际运行的时候,按照这种变体形式可以减少计算量,因为对于每个隐层节点来说,$\frac{\gamma}{\sqrt{\operatorname{Var}[x]+\varepsilon}}$和$\frac{\gamma \cdot E[x]}{\sqrt{\operatorname{Var}[x]+\varepsilon}}$都是固定值,这样这两个值可以事先算好存起来,在推理的时候直接用就行了。
5. Batch Normalization的好处
BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度
BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度
BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定
BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题
BN具有一定的正则化效果
在Batch Normalization中,由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计,尽管每一个batch中的数据都是从总体样本中抽样得到,但不同mini-batch的均值与方差会有所不同,这就为网络的学习过程中增加了随机噪音,与Dropout通过关闭神经元给网络训练带来噪音类似,在一定程度上对模型起到了正则化的效果