论文阅读：Decoupled Weight Decay Regularization

训练神经网络时会使用 weight decay，decay，词义是『 衰减、减小』，weight decay，使网络层的参数减小，以使得网络获得更好的性能，也避免梯度爆炸的情况出现。现在的各种优化器，如 SGD, Adam 等，在使用的时候都会有一个参数 weight_decay。现在的各种框架中，实际上是用 L2 正则化来实现 weight decay 的，也就是说，这些框架认为 weight decay 和 L2 正则化是等价的。在说到 L2 正则化的作用时，也经常会提到 L2 正则化可以使得权重减小，起到 weight decay 的作用。本文做的工作，首先证明了 weight decay 在 SGD 优化器中与 L2 正则化确实是等价的，但在 Adam 优化器中却不是这样，因此现在在 Adam 优化器中也用 L2 正则化来实现 weight decay 是有问题的，并没有真正起到 weight decay 的作用，会降低 Adam 优化器的泛化性能。针对这个问题，作者又提出了改进措施。

论文标题：Decoupled Weight Decay Regularization

作者：Ilya Loshchilov, Frank Hutter

发表于 ICLR 2019

地址：arXiv , OpenReview

1. SGD 和 Adam 优化器中的 weight decay 与 L2 正则化

首先给出 weight decay 的定义，这个定义是在文章 ^{Hanson & Pratt (1988)} 中被提出的：

$$\boldsymbol{\theta}_{t+1}=(1-\lambda) \boldsymbol{\theta}_{t}-\alpha \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right) \,.$$

这个公式实际上就是在更新参数的时候，除了减去梯度外，还直接减去一个系数乘以参数本身，这样 weight 就 decay 了。其中 $\lambda$ 是权重衰减系数。$\nabla f_t (\boldsymbol{\theta}_t)$ 是第 $t$ 个 batch 时的梯度。

1.1. 解耦 SGD

首先给出一个命题：

Proposition 1: 对于 SGD 优化器，使用 weight decay，等价于使用 L2 正则化：

$$f_{t}^{r e g}(\boldsymbol{\theta})=f_{t}(\boldsymbol{\theta})+\frac{\lambda^{\prime}}{2}\|\boldsymbol{\theta}\|_{2}^{2} \,,$$

其中 $\lambda^{\prime} = \frac{\lambda}{\alpha}$。式中的 reg 是 regulation 的意思，而不是 regression。

证明如下：

对 L2 正则化的式子求导，得：

$$\nabla f_{t}^{\mathrm{reg}}\left(\boldsymbol{\theta}_{t}\right)=\nabla f_{t}\left(\boldsymbol{\theta}_{t}\right)+\lambda^{\prime} \boldsymbol{\theta}_{t} \,.$$

做一下梯度下降，在学习率为 $\alpha$ 的情况下，得到：

$$\boldsymbol{\theta}_{t+1} \leftarrow \boldsymbol{\theta}_{t}-\alpha \nabla f_{t}^{\mathrm{reg}}\left(\boldsymbol{\theta}_{t}\right)=\boldsymbol{\theta}_{t}-\alpha \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right)-\alpha \lambda^{\prime} \boldsymbol{\theta}_{t} \,.$$

与 weight decay 的公式比较，只需要满足 $\lambda = \alpha \lambda^{\prime}$，二者就是等价的，即 $\lambda^{\prime} = \frac{\lambda}{\alpha}$。

也就是说，只要把 L2 正则化的系数设置一下，在 SGD 里就可以用 L2 正则化代替 weight decay。

当然从这个式子也可以看出，使用 L2 正则化代替 weight decay 时，L2 的系数如何选取，是跟学习率 $\alpha$ 有关的，这样这个系数跟学习率就是 coupled。比如说我想要设置大小为 $\lambda$ 的 weight decay 系数，现在的深度学习框架里都用 L2 正则化来代替，也就是要事先设置 L2 正则化系数，这个系数需要根据学习率的大小来设置，如果学习率的大小是变的，那就比较好设置；然而现在的学习率通常是变化的，这样设置了固定的 L2 正则化系数后，实际的 weight decay 系数也是在改变的。

文章标题说 Decoupled Weight Decay Regularization，就是要把这个系数和学习率 decouple（解耦）。因此作者引入了下面的算法：

其中第 6 行是 L2 正则化算法，在计算梯度的时候就把正则项的导数加上，并根据这个导数计算动量，注意这一行里的 $\lambda$ 是 L2 正则化系数。解耦的方法是不在计算梯度的时候加上 L2 正则项，事实上压根就不用正则项，直接在第 9 行直接对 weight 进行 decay，即 $-\eta_t \lambda \boldsymbol{\theta}_{t-1}$，抛开 $\eta_t$ 不看，实际上就是 weight decay 的定义，第 12 行里的 $\lambda$ 是 weight decay 的系数。这样 weight decay 的系数和学习率就完全解耦（decouple）了。解耦后的 SGD 算法叫做 SGDW (SGD with decoupled Weight decay)。

需要说明的这里的 $\eta_t$，是用于调整学习率的，调整学习率不是直接对 $\alpha$ 本身做调整（这个 $\alpha$ 是初始学习率，设定之后就不再变动了），但是每个 step 使用学习率的时候，都会给它乘以一个数 $\eta_t$（文中称其为 multiplier），通过 $\operatorname{SetScheduleMultiplier}$ 函数调整每个 step 的 $\eta_t$，从而间接起到调整实际学习率的效果。

1.2. 解耦 Adam

命题 1 证明了对于 SGD 优化器，使用 weight decay 等价于使用 L2 正则化。作者提出对于自适应优化器（不止 Adam，AdaGrad, RMSProp 等也是），weight decay 与 L2 正则化不等价，因此实际上不能用 L2 正则化来代替 weight decay。

Proposition 2: 对于自适应梯度优化器， weight decay 与 L2 正则化不等价。设对于优化器 $O$，其不带 weight decay 的梯度迭代公式为：

$$\boldsymbol{\theta}_{t+1} \leftarrow \boldsymbol{\theta}_{t}-\alpha \mathbf{M}_{t} \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right) \,.$$

带 weight decay 的迭代公式为：

$$\boldsymbol{\theta}_{t+1} \leftarrow(1-\lambda) \boldsymbol{\theta}_{t}-\alpha \mathbf{M}_{t} \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right) \,,$$

因为优化器是自适应的，显然 $\mathbf{M}_{t} \neq k \mathbf{I}$ (where $\left.k \in \mathbb{R}\right)$。

仿照 SGD中的，现在想用在损失函数 $f_t$ 上再加 L2 正则化来代替 weight decay，即用 $f_{t}^{r e g}(\boldsymbol{\theta})=f_{t}(\boldsymbol{\theta})+\frac{\lambda^{\prime}}{2}|\boldsymbol{\theta}|_{2}^{2}$ 来代替 $\boldsymbol{\theta}_{t+1} \leftarrow \boldsymbol{\theta}_{t}-\alpha \mathbf{M}_{t} \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right)$ 中的 $f_t$，使得这个迭代公式与带 weight decay 的迭代公式等价。然而这样的 L2 正则化系数 $\lambda^{\prime}$ 是不存在的。

证明如下：

对使用 L2 正则化的式子求导，得：

$$\boldsymbol{\theta}_{t+1} \leftarrow \boldsymbol{\theta}_{t}-\alpha \lambda^{\prime} \mathbf{M}_{t} \boldsymbol{\theta}_{t}-\alpha \mathbf{M}_{t} \nabla f_{t}\left(\boldsymbol{\theta}_{t}\right) \,.$$

如果要使这个式子与带 weight decay 的迭代公式等价，则要求满足

$$\lambda \boldsymbol{\theta}_{t}=\alpha \lambda^{\prime} \mathbf{M}_{t} \boldsymbol{\theta}_{t} \,.$$

为了满足上式，需要对于所有 step 的 $\boldsymbol{\theta}_t$ 存在 $\mathbf{M}_{t}=k \mathbf{I}$，其中 $k \in \mathbb{R}$。而根据前提条件，这个是无法满足的。

因此不存在 L2 正则化系数 $\lambda^\prime$ 使得在自适应优化器上 L2 正则化等价于 weight decay。

对于 Adam 优化器，作者同样提出解耦 weight decay 的系数，而不是使用 L2 正则化，如下面的算法流程所示。

作者提出，在 Adam 优化器中直接使用 L2 正则化代替 weight decay 时，会使得不同的 weight 的 decay 程度不一样，而从 weight decay 的原始公式来看，不同的权重的 decay 系数都应该是相同的 $\lambda$。这个原因可以从 Algorithm 2 中的公式看出来，使用 L2 正则化时，L2 norm 的梯度是一起加到总梯度里的（第 6 行），回到第 12 行，分母上的 $\hat{\boldsymbol{v}_t}$ 用来调整权重「梯度」下降的多少（「梯度」累计值越大的权重，下降的越少），这里用了加引号的梯度，是因为这里的「梯度」不仅包含了损失函数的梯度，还包含了 L2 norm 的梯度（在用 L2 正则化代替 weight decay 时，L2 norm 的梯度就代表了 weight 的 decay），也就是说，weight decay 的程度，也会受到梯度累计值的大小影响。具体来说，梯度累计值越大的权重，被正则化的越少（也就是 weight decay 的程度越少）。这是不合理的。

用公式来理解一下上面一段话。把第 6 行和第 7 行代入第 12 行，得到：

$$\begin{align} \boldsymbol{\theta}_{t} &\leftarrow \boldsymbol{\theta}_{t-1}-\eta_{t}\left(\alpha \hat{\boldsymbol{m}}_{t} /\left(\sqrt{\hat{\boldsymbol{v}}_{t}}+\epsilon\right)\right. \\ &= \boldsymbol{\theta}_{t-1} - \eta_t \alpha \frac{\boldsymbol{m}_t / (1-\beta^t_1)}{\sqrt{\hat{\boldsymbol{v}}_{t}}+\epsilon} \\ &= \boldsymbol{\theta}_{t-1} - \eta_t \alpha \frac{\beta_{1} \boldsymbol{m}_{t-1}+\left(1-\beta_{1}\right) \boldsymbol{g}_{t}}{(1-\beta^t_1)(\sqrt{\hat{\boldsymbol{v}}_{t}}+\epsilon)} \\ &= \boldsymbol{\theta}_{t-1} - \eta_t \alpha \frac{\beta_{1} \boldsymbol{m}_{t-1}+\left(1-\beta_{1}\right) (\nabla f_{t}\left(\boldsymbol{\theta}_{t-1}\right)+\lambda \boldsymbol{\theta}_{t-1})}{(1-\beta^t_1)(\sqrt{\hat{\boldsymbol{v}}_{t}}+\epsilon)} \,. \end{align}$$

看右上角的 $\lambda \boldsymbol{\theta}_{t-1}$，这应该是起到 weight decay 作用的，但它的实际作用受到分母项 $\sqrt{\hat{\boldsymbol{v}}_t}$ 的影响，$\sqrt{\hat{\boldsymbol{v}}_t}$ 有更大的值，就会使调整后的 $\frac{\lambda \boldsymbol{\theta}_{t-1}}{\sqrt{\hat{\boldsymbol{v}}_{t}}}$ 更小，在这个方向上 $\boldsymbol{\theta}$ 被正则化地更少，这是不合理的。而使用解耦后的公式，weight decay 就不会收到积累的历史梯度值影响，各个权重的 decay 程度都是一样的。

关于 Algorithm 2 中的第9 行和第 10 行，以前我知道是对梯度累计值和梯度平方累计值做一个修正，目的是使对二者的有偏估计变成无偏估计，但一直不理解为什么，现在看到一种解释：

当 $t$ 足够大时，$\hat{\boldsymbol{m}}_t = \hat{\boldsymbol{m}}$。初始时刻 $t = 1$, $\beta_1 = 0.9$, $\hat{\boldsymbol{m}}_0 = 0$, $\hat{\boldsymbol{m}}_1 = 0.9 \cdot \hat{\boldsymbol{m}}_0 + 0.1 \cdot \hat{\boldsymbol{g}}_1 = 0.1 \cdot \boldsymbol{g}_1$，这显然不合理，但是除以 $1 - \beta_1^t = 1 - 0.9 = 0.1$ 后 $\hat{\boldsymbol{m}}_1 = \boldsymbol{g}_1$，这是比较合理的。对于第 10 行同理。

这段理解来自 知乎：都9102年了，别再用Adam + L2 regularization了

2. 实验

2.1. Adam 优化器上 decoupled weight decay 和 L2 正则化的对比

使用 decoupled weight decay 的方法称为 AdamW，使用 L2 正则化的方法就称为 Adam，使用了三种不同的学习率调整策略：（1）固定学习率；（2）阶梯下降（drop-step，不知如何翻译）的学习率；（3）余弦退火（cosine annealing）策略。对比图如下：

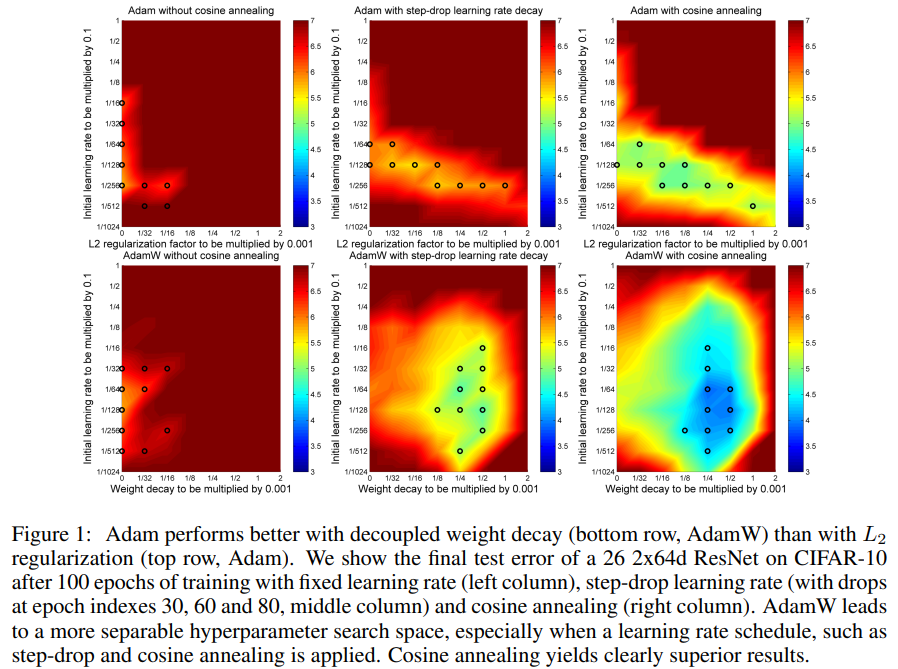
2.2. Adam 优化器和 SGD 优化器的对比

整体对比图如下。文中提到，对于使用 L2 正则化的情况，两种优化器的最优超参数区域（basin）都是呈对角线的，这表明横纵坐标的两个超参数是相互依赖的，如果固定一个超参数而调整另一个，会使得结果恶化。而使用 decoupled weight decay 的情况下，最有超参数区域是与坐标轴平行的，这样两个超参数是独立的，可以固定一个调整另一个，仍然可以落在最优解区域内。

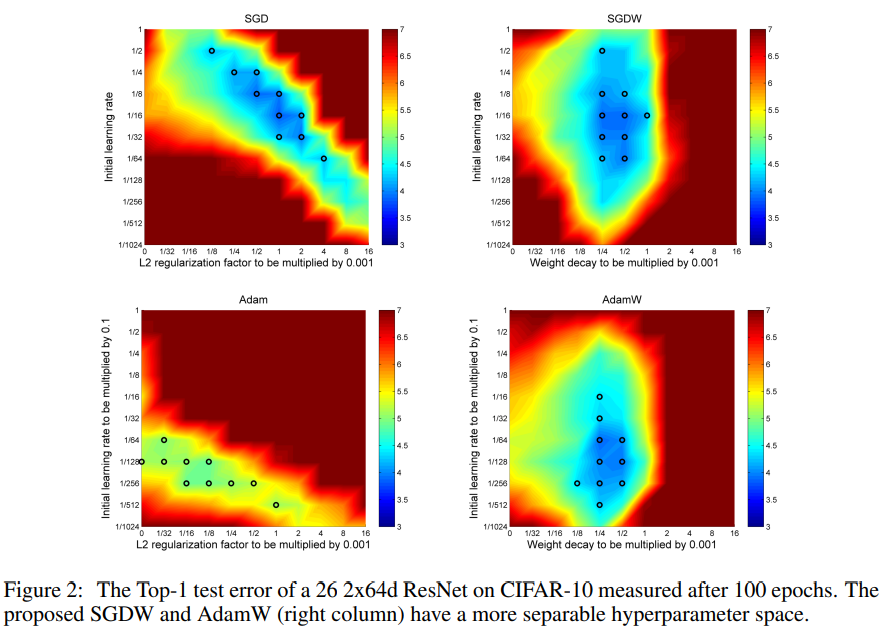
3. 应用

目前 BERT 训练采用的优化方法就是 AdamW，对除了 LayerNorm，bias 项之外的模型参数做 weight decay。

根据我的理解，现在训练网络，优化器使用 AdamW，学习率调整机制可以使用 CosineAnnealingWarmupRestarts，另外 VilBERT 工作中使用的是 WarmupLinearSchedule。

4. 参考文献

^{Hanson & Pratt (1988)}. Hanson, Stephen, and Lorien Pratt. “Comparing biases for minimal network construction with back-propagation.” Advances in neural information processing systems 1 (1988): 177-185. ↩