本文为通常所说的 SimCLR
论文标题:A Simple Framework for Contrastive Learning of Visual Representations
作者:Ting Chen, Simon Kornblith, Mohammad Norouzi, Geoffrey Hinton
发表于 ICML 2020
地址:arXiv
参考代码:GitHub,这是第三方代码(PyTorch),不是作者提供的 TensorFlow 代码
1. 核心思想
本文在摘要和 Introduction 中提到,本文的主要贡献为:
- 对于无监督学习来说,组合使用数据增强很重要,即需要强有力的数据增强(指在产生 multi-view pair 的时候)
- 获得特征表示后再加一个非线性变化(就是全连接层)之后再计算对比损失,可以提高特征表示的能力
- 相比于有监督学习,使用更大的 batch size 和更深、更宽的网络对无监督对比学习的特征表示能力提高更大
2. 总体框架
如下图所示:
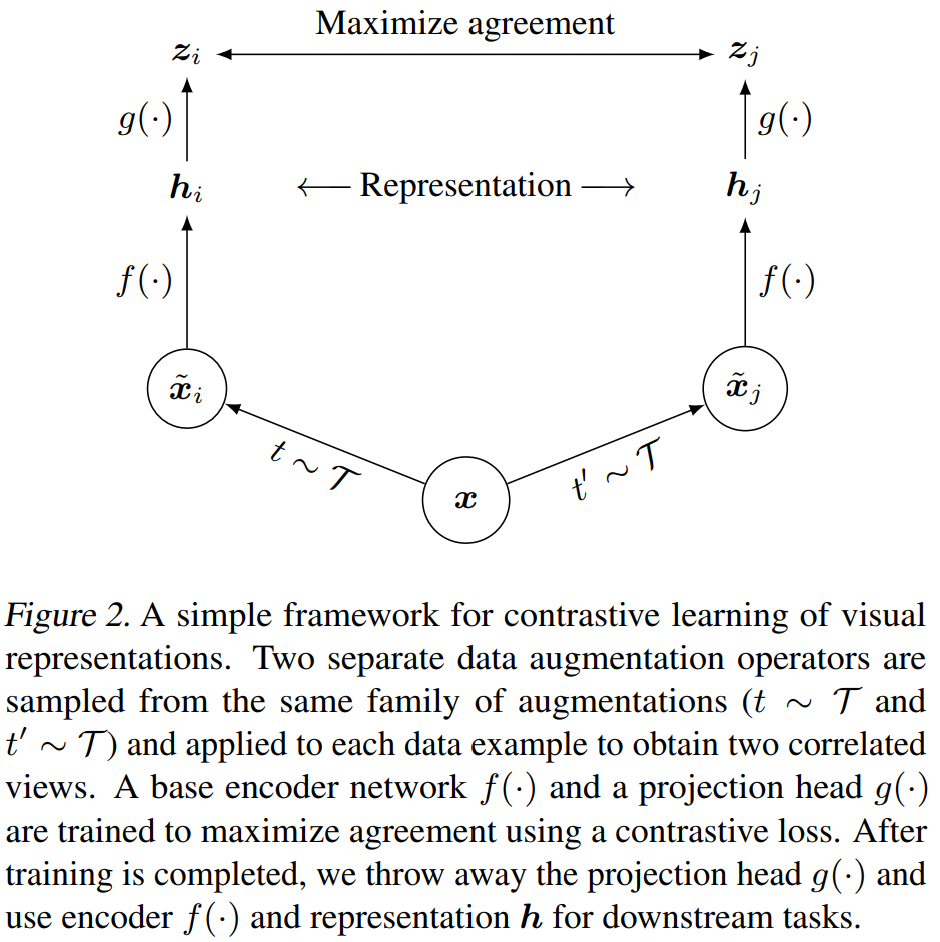
首先将图片做随机变换作为 multi-view 的 positive pair,本文使用了 3 中随机变换:
- random cropping followed by resize back to the original size
- random color distortions
- random Gaussian blur
图片经过一个 encoder 提取特征 $\boldsymbol{h}_i$ 和 $\boldsymbol{h}_j$,编码器即图中的 $f(\cdot)$,本文使用的是 ResNet
特征表示后再加一个小的 projection head $g(\cdot)$,用于将特征映射为 $\boldsymbol{z}_i$,本文使用简单的 MLP 作为 head:
对比损失使用的也是 InfoNCE,具体来说,对于一个 batch,有 $N$ 个样本,经过变化得到 $2N$ 个数据。对于每个 positive pair,其余的 $2(N-1)$ 个数据都作为负样本。两个样本之间的相似度用余弦相似度计算:$\operatorname{sim}(\boldsymbol{u}, \boldsymbol{v})=\boldsymbol{u}^{\top} \boldsymbol{v} /|\boldsymbol{u}||\boldsymbol{v}|$. 对于一个正样本对 $(i, j)$,对比损失会希望 $j$ 和 $i$ 的相似度最大,而与其他数据的相似度比较小,损失函数定义为:
这里的 $\mathbb{1}_{[k \neq i]}$ 是指示函数(indicator function),显然分母中不包含 $i$ 自己与自己的相似度,所以 数据 $i$ 是要在除自己以外的 $2(N-1)$ 个数据中分辨出 $j$ 来。$\tau$ 是温度系数,用于做 scaling。这个在很多文章中的 InfoNCE loss 中都用到过,通过视频 B站-未来亦可期-CV 中的解释,我理解了这个的用处。这个损失其实是类似于 Softmax 函数的,但是分子和分母中的每一项不是网络直接输出的概率值,而是余弦相似度,余弦相似度范围为 $[-1,1]$,经过 exponential 后,其值相差并不大,$e^1=2.718$, $e^{-1} = 0.367$,差距并不大。考虑最极端的情况,假设 $i$ 与 $j$ 的相似度为 1(这已经是最大了),而与其他样本 $k \neq j$ 且 $k \neq i$ 的相似度为 -1,batch size 为 256 的话,分子会远远小于分母,使得 $i$ 和 $j$ 的相似度无法凸显出来。但加了温度系数就不一样了,这个 $\tau$ 一般是比较小的值,比如 MoCo 中取值是 0.07,这样就能把 positive pair 和 negative pair 的相似度经过指数后拉开差距(毕竟指数增长是很迅猛的)。另外文中提到,这个损失对所有 pair 都是计算的,即 $(i, j)$ 和 $(j, i)$ 都要分别计算损失。
下面是文中给出的算法代码:

上面这个算法中,是将奇数序号的样本和偶数序号的样本分别作为一个 image 的两个不同的 view,这样对于一张图像,它的两个 augmentation 之后的 view 是相邻的。随后计算一个相似度矩阵,batch size 为 $N$ 的情况下,共有 $2N$ 个样本,相似度矩阵为 $2N \times 2N$ 的,即样本之间两两计算相似度,包括自己与自己。但在计算损失的,自己与自己的相似度是不用的。上面算法中的损失计算相当于按行求 Softmax,当然前提是去除自己与自己的那个相似度,而 label 就是与自己来自同一图像的样本的序号。对每一行都这样操作,这样就会有 $\ell(2k-1,2k) + \ell(2k, 2k-1)$ 了。
我找到一个 PyTorch 版本的 SimCLR 实现,下面是关于损失计算的代码,主要看一下实现技巧,代码中的中文注释都是我添加的注释:
1 | def info_nce_loss(self, features): |
这里的代码返回 logits 和 labels,并未直接计算 loss,在训练代码中再计算 loss:
1 | features = self.model(images) |
其中 self.criterion = torch.nn.CrossEntropyLoss().to(self.args.device),就是交叉熵损失函数。
本文选择的 batch size 从 256~8192,这样可以提供足够多的负样本(8192 时负样本数量为 $16382=8192\times2-2$),作者说 batch size 很大的时候,SGD/Momentum with linear learning rate scaling 优化器不太行,因此使用了 LARS 优化器You et al.,2017 。
You et al.,2017 . You, Y., Gitman, I., and Ginsburg, B. Large batch training of convolutional networks. arXiv preprint arXiv:1708.03888, 2017. ↩
关于 Glibal BN:作者说多卡训练的时候,所有的正样本都在一张卡上,这样会造成信息泄露使得模型学习到一些捷径(模型坍缩)。作者使用的方法是将所有卡上 BN 层计算的 mean 和 variance 加在一块,然后每块卡上的数据都用这个均值来计算。这不同于 MoCo 中用的 shuffle BN。
文中使用的数据集为 ImageNet,部分实验也在 CIFAR-10 上做了。本文只做了分类实验,使用的规则为 linear probe。
一些默认设置:
| 设置项 | 设置内容 |
|---|---|
| augmentation | random crop and resize (with random flip), color distortions, Gussian blur |
| encoder | ResNet-50 (特征表示维度为 2048) |
| 优化器 | LARS, weight decay = $10^{-6}$ |
| 学习率 | 4.8 (=0.3 × Batchsize / 256) |
| batch size / epochs | 4096 / 100 |
| 训练策略 | linear warmup for the first 10 epochs, cosine decay schedule without restarts |
3. 数据增强很重要
这里说的数据增强指的是产生 mulit-view 的时候使用的数据增强方法。另外说一句,这种通过数据增强获得不同 view 用来做对比的无监督学习方式适合于 object-centric 的图片,即一张图片只有一个占据主导地位的物体,这样可以保证不同的增强之后得到的 view 仍然是具有高度相关性的。对于自然场景中的多目标图像,这种方法不一定适合,可以参见 NeurIPS 2021 论文 Unsupervised Object-Level Representation Learning from Scene Images 及 相应的讲解视频。
下图展示了文中使用的一些数据增强手段:

注意图中也说了,这里虽然展示了这么多增强手段,但文中训练时只用了 random crop (with flip and resize), color distortion, and Gaussian blur。
为了评估不同的数据增强方式的效果,文中做了 ablation study。因为 ImageNet 中的图片都要做 crop and resize,为了能够验证某种数据增强方法(可能是一种增强方法,也可能是组合)的作用,首先对于所有图片,都先做 crop and resize,这样得到的图片再成为两个不同的 view:这里用了不对称的方式,其中一个 view 不做任何变换,另一个 view 使用一种变换方式,这样可以单方面地验证某种数据增强方法的作用(当然这种情况下训练效果会下降)。
文中比较了使用不同的(单个)数据增强方法在 ImageNet 上预训练后做 linear evaluation 的 top-1 accuracy,如下图所示:
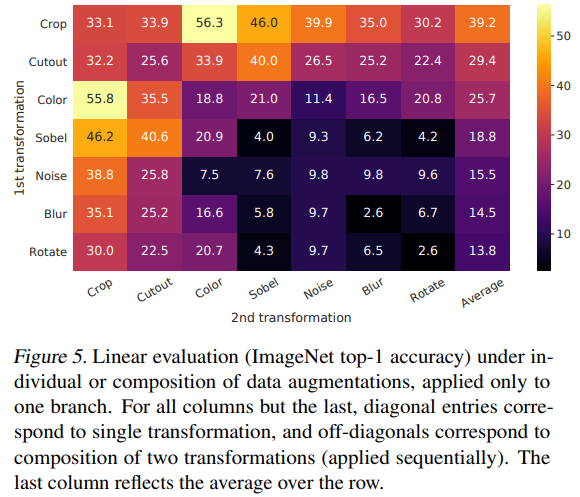
可以看出,只使用一个数据增强(而不是两种组合)时,效果都不太行(这可以从对角线看出来)。
random cropping + random color distortion 的数据增强组合方式效果最突出。文中猜测,只使用 random crop 时效果不好,可能是因为同一张图片 crop 出来的不同 patch 的颜色分布基本一致,而不同的图片其分布则有所不同,这样模型可能会学到这样的捷径,而没有真的提取到有用的特征。
另外,作者通过实验认为,相比于有监督学习,数据增强对无监督学习的性能提升更大。
4. 结构设计
4.1. Unsupervised contrastive learning benefits (more) from bigger models
作者首先做了实验表明,无监督学习更受益于大模型,对于有监督学习来说,模型容量越大带来的增益不如无监督学习:
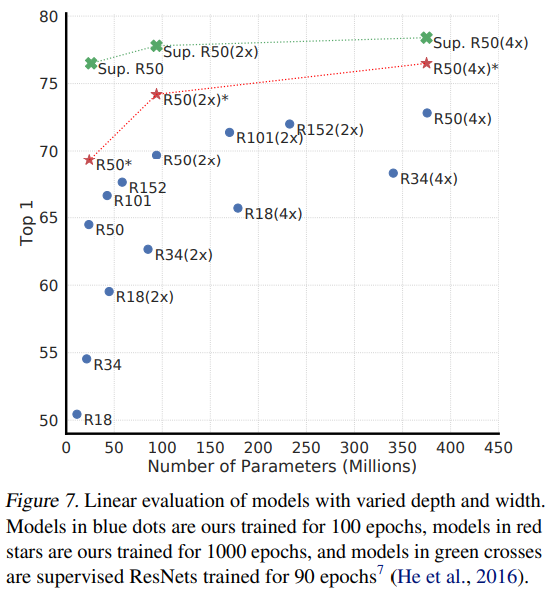
4.2. A nonlinear projection head improves the representation quality of the layer before it
下图表明使用非线性 projection head 的效果好于使用线性 projection head 好于不使用 projection head:
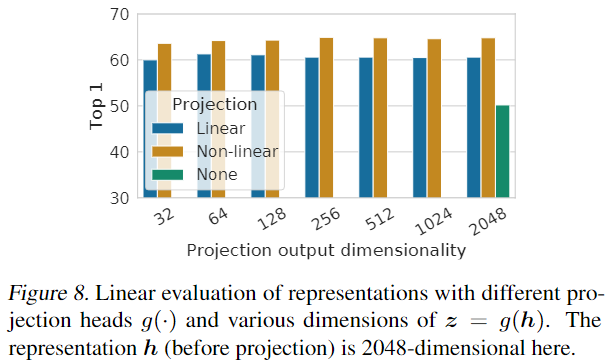
作者猜想加 projection head 再计算损失函数之所以有效,是因为 projection head 可以去除对于下游任务有用的信息,如物体的颜色或角度,这样,projection head 之前的那个特征表示就可以包含更多的信息(用于做特征表示迁移到下游任务)。
注意本文使用的 projection head 只是 $W^{(2)}\sigma (W^{(1)}\boldsymbol{h}_i)$,其中没有使用 BN 层。
5. batch size 的作用
如下图所示:
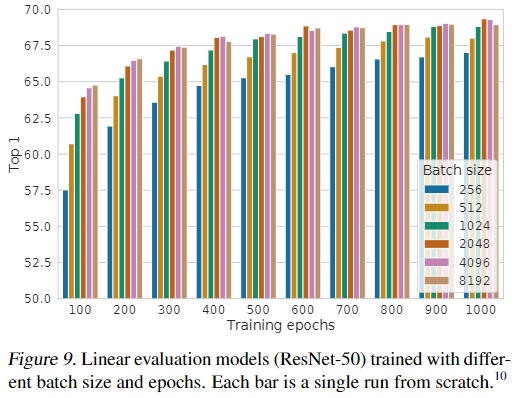
在 epoch 较少时,大的 batch size 起的作用很显著,当 epoch 比较多时,不同的 batch size 之间的差异性就不是特别明显了。
6. 实验结果对比
本文使用了 ResNet-50 的 3 种不同宽度的模型(1×, 2 ×, 4×),训练了 1000 个 epoch。
本文只做了分类实验,没有检测、分割等下游任务。
6.1. Linear evaluation
结果如下:
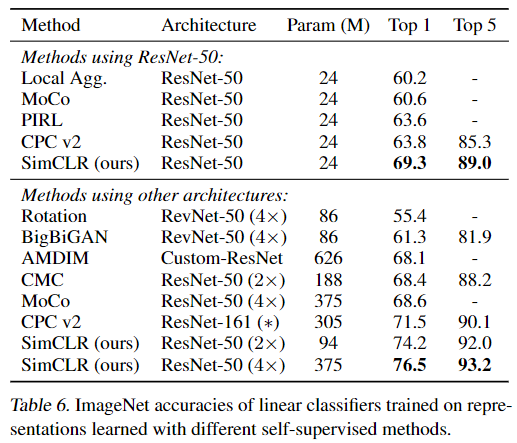
6.2. Semi-supervised learning
半监督学习指使用 ImageNet 中 1%(每类 ~12.8 张图片) 和 10%((每类 ~128 张图片)) 的数据对网络进行 fine tune,下面是结果对比:
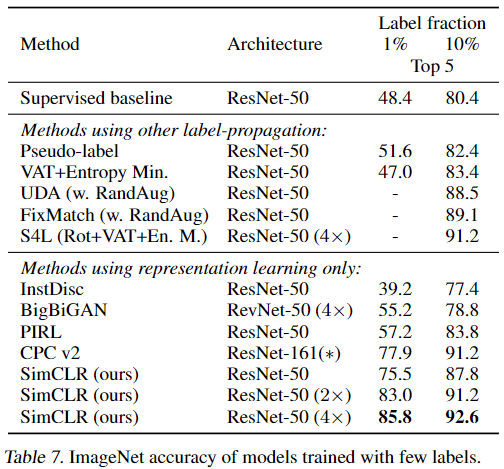
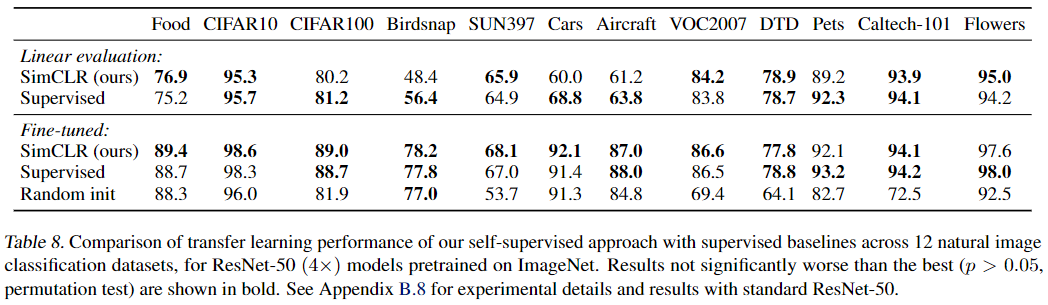
6.3. Transfer learning
迁移到其他数据集上分类。使用的模型为 ResNet-50 4×,对每个数据集都调整了超参数的选择。