真正理解 Normalization

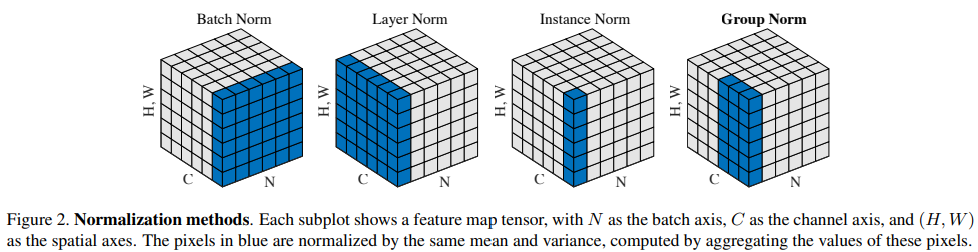
我对深度学习中用到的几种 Normalization 的原理一直了解得不是很清晰，只有个模糊的概念。网上有很多文章介绍相关内容，但我觉得写的都不好，都是模模糊糊的套话，并没有真正深入解释，我们都知道要求均值求标准差，但具体是在哪些维度求呢，并没有讲清楚。很多人喜欢用何恺明在 Group Normalization 中作的一张图（如下），但这个图其实不好看懂，尤其对于本来就不甚清楚的人（就是我）来说。为了清楚这些 Normalization 的原理，我看了一下它们的实现代码，并根据代码自己画了一些示意图，还自己写了简单的实现代码与 PyTorch 中的 API 对比来验证我的理解的正确性。

本文只介绍了三种 Normalization: Batch Normalization, Layer Normalization, Group Normalization，还有一个 Instance Normalization 没有介绍，因为这个主要用在图像迁移里，对于大部分场合来说并不常用，所以我暂时也没打算去深入了解。

1. Batch Normalization

Batch Normalization 是沿通道维度计算均值和标准差，沿通道维度是说，把当前 batch 里每个样本这个通道上的所有值放在一块计算均值和标准差。注意对于 4-D 或者 3-D 的 Tensor 来说，对于一个样本，每个通道上的数目并不仅仅是 1，比如 4-D 的 Tensor，一个通道上有 $H \times W$ 个 element，并不是一个 batch 里样本的同一通道上的每个位置都计算这个位置的均值和标准差，而是把这个通道上的所有 element 放在一起看。

下面是一个 4-D Tensor with shape $(B, C, H, W)$ 计算均值和标准差的示意图，计算得到的均值和方差的形状是 $(C,)$，再广播成输入的形状进行计算。

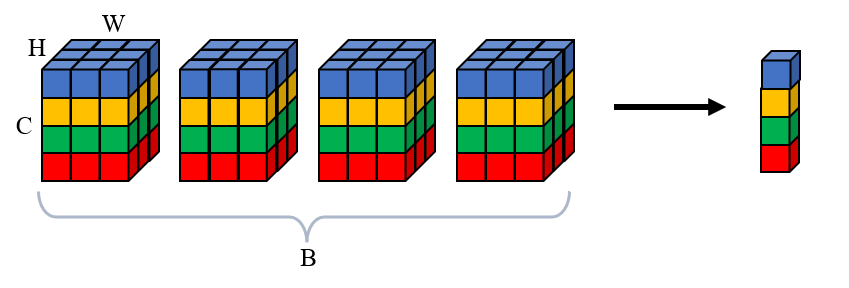
为了保证非线性，还要再 scale and shift，用两个参数 $\gamma$ 和 $\beta$，二者的形状是 $(C,)$

计算方差（或标准差）是有偏的，即除以 $B$ 而不是 $B-1$

对于不同形状的输入，计算规则如下：

一个 batch 的图片输入 $X \in \mathbb{R}^{B \times C \times H \times W}$, $\gamma \in \mathbb{R}^C$, $\beta \in \mathbb{R}^C$:
$\mathrm{BN}(X)=\gamma \frac{X-\underset{B, H, W}{\mathbb{E}}[X]}{\sqrt{\underset{B, H, W}{\operatorname{Var}}[X]+\epsilon}}+\beta$
一个 batch 的 sequence embeddings 输入 $X \in \mathbb{R}^{B \times C \times L}$, $\gamma \in \mathbb{R}^C$, $\beta \in \mathbb{R}^C$:
$\mathrm{BN}(X)=\gamma \frac{X-\underset{B, L}{\mathbb{E}}[X]}{\sqrt{\underset{B, L}{\operatorname{Var}}[X]+\epsilon}}+\beta$
一个 batch 的 embeddings 输入 $X \in \mathbb{R}^{B \times C}$, $\gamma \in \mathbb{R}^C$, $\beta \in \mathbb{R}^C$:
$\mathrm{BN}(X)=\gamma \frac{X-\underset{B}{\mathbb{E}}[X]}{\sqrt{\underset{B}{\operatorname{Var}}[X]+\epsilon}}+\beta$

因为 BN 在 2D 图像处理中比较常用，所以看一下 PyTorch 中的 torch.nn.BatchNorm2d:

torch.nn.BatchNorm2d(num_features, 
                     eps=1e-05, 
                     momentum=0.1, 
                     affine=True, 
                     track_running_stats=True, 
                     device=None, dtype=None)

num_features: 通道数
eps: 防止零除
affine: 是否 scale and shift，这两个参数 $\gamma$ 和 $\beta$ 是可学习的参数，在代码中应该用 nn.Parameter 包裹这两个 Tensor
1
2
3
4
# init
if self.affine:
self.scale = nn.Parameter(torch.ones(channels))
self.shift = nn.Parameter(torch.zeros(channels))

momentum: 计算 running_mean 和 running_var，用于推理的时候使用，running_mean 和 running_var 不应该参与梯度计算，所以应该加入 buffer 中

track_running_stats: 是否计算 running_mean 和 running_var，默认是计算的。如果设置为 False，则在推理的时候也当场计算参与推理的 batch 的 mean 和 var

# init
if self.track_running_stats:
    self.register_buffer('running_mean', torch.zeros(channels))
    self.register_buffer('running_var', torch.ones(channels))

# update
if self.track_running_stats:
	self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * mean
	self.running_var = (1 - self.momentum) * self.running_var + self.momentum * var

自己实现简单的代码验证一下：

import torch
import torch.nn as nn

x = torch.randn(3, 4, 5, 5)

# 这里用于验证的时候要把 affine 设为 False，因为 PyTorch 中
# 是用 torch.empty() 初始化 scale 和 shift 的
y_bn = nn.BatchNorm2d(4, affine=False)(x)

x_mean = torch.mean(x, dim=(0, 2, 3), keepdim=True)  # shape=(1, 4, 1, 1)
x_std = torch.std(x, dim=(0, 2, 3), unbiased=False, keepdim=True)# shape=(1, 4, 1, 1)
eps=1e-5
y_verify = (x - x_mean) / (x_std + eps)

print(torch.sum((y_bn - y_verify) < 1e-4).item())

"""
outputs:
300
"""

代码实现可以参考 labml.ai-batch_norm

2. Layer Normalization

Layer Normalization 主要被用于 NLP 领域，它跟 batch size 无关，是在每个样本的 feature 上做 normalization，这里说的 feature 具体指代什么，可以根据不同的输入来决定（用 normalizaed_shape 来指定）。在 NLP 任务中，一般是将每个词的 embedding 做 normalization。这是比较符合直觉的，因为不能一个 batch 的不同 sample 之间做 normalization，同样在一个 sequence 里面做 normalization 也不行，因为一个 sequence 里会有 padding，把 padding 和其他词的 embedding 一起做 normalization 是不合理的，只能是每个词自己做 normalization。

下面是一个 3-D Tensor with shape $(B, L, C)$ 计算均值和标准差的示意图，计算得到的均值和方差的形状是 $(B,L)$，再广播成输入的形状进行计算。即有 $B$ 个句子，每个句子长度为 $L$，每个词的 embedding size 为 $C$。

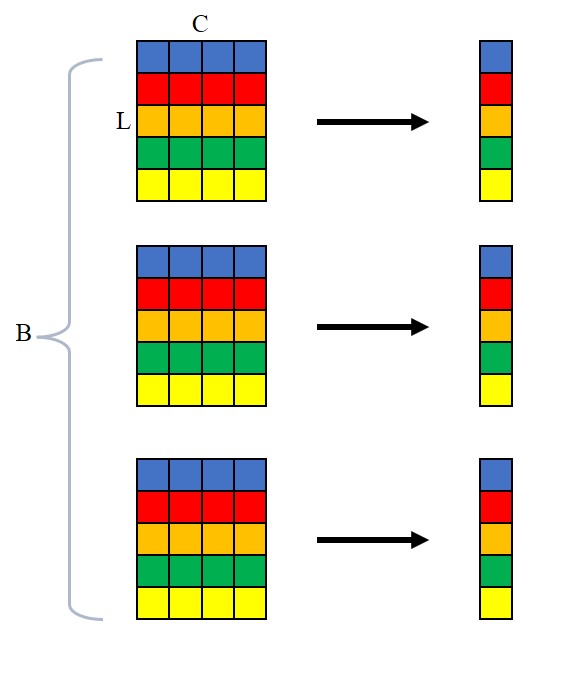
同样，Layer Normalization 中也会加上 scale and shift，但与 Batch Normalization 不同，这个是 element-wise 的，也就是 scale and shift 的形状与参与 normalization 的那部分 feature 维度相同。

计算方差（或标准差）同样是有偏的

对于不同形状的输入，计算规则如下：

一个 batch 的 sequence embeddings 输入 $X \in \mathbb{R}^{B \times C \times L}$, $\gamma \in \mathbb{R}^C$, $\beta \in \mathbb{R}^C$:
$\mathrm{LN}(X)=\gamma \frac{X-\underset{C}{\mathbb{E}}[X]}{\sqrt{\underset{C}{\operatorname{Var}}[X]+\epsilon}}+\beta$
一个 batch 的 embeddings 输入 $X \in \mathbb{R}^{B \times C}$, $\gamma \in \mathbb{R}^C$, $\beta \in \mathbb{R}^C$:
$\mathrm{LN}(X)=\gamma \frac{X-\underset{C}{\mathbb{E}}[X]}{\sqrt{\underset{C}{\operatorname{Var}}[X]+\epsilon}}+\beta$
一个 batch 的图片输入 $X \in \mathbb{R}^{B \times C \times H \times W}$, $\gamma \in \mathbb{R}^{C \times H \times W}$, $\beta \in \mathbb{R}^{C \times H \times W}$:
$\mathrm{LN}(X)=\gamma \frac{X-\underset{C, H, W}{\mathbb{E}}[X]}{\sqrt{\underset{C, H, W}{\operatorname{Var}}[X]+\epsilon}}+\beta$

PyTorch 中的 Layer Normalization 不分什么 1-D, 2-D 的，统一用 torch.nn.LayerNorm:

torch.nn.LayerNorm(normalized_shape, 
                   eps=1e-05, 
                   elementwise_affine=True, 
                   device=None, dtype=None)

normalized_shape: 参与 normalization 的那几个维度的形状，一般都是后面几个维度。normalized_shape 可以是 int, list 或 torch.Tensor，如果是 int 就转成 list。比如 NLP 中一个输入序列的 shape 是 (B, L, C)，则 normalized_shape 就是 C 或 [C]，这样参与 normalization 的 dim 就是 -1.
eps: 防止零除
elementwise_affine: 是否 scale and shift，这两个参数 $\gamma$ 和 $\beta$ 是可学习的参数，在代码中应该用 nn.Parameter 包裹这两个 Tensor
1
2
3
if self.elementwise_affine:
self.gain = nn.Parameter(torch.ones(normalized_shape))
self.bias = nn.Parameter(torch.zeros(normalized_shape))

自己实现简单的代码验证一下：

import torch
import torch.nn as nn

batch_size = 3
seq_len = 5
embedding_dim = 4
x = torch.randn(batch_size, seq_len, embedding_dim)

y_ln = nn.LayerNorm(normalized_shape=[embedding_dim], elementwise_affine=False)(x)

x_mean = torch.mean(x, dim=-1, keepdim=True)  # shape=(3, 5, 1)
x_std = torch.std(x, dim=-1, unbiased=False, keepdim=True)  # shape=(3, 5, 1)
eps=1e-5
y_verify = (x - x_mean) / (x_std + eps)

print(torch.sum((y_ln - y_verify) < 1e-4).item())

"""
outputs:
60
"""

3. Group Normalization

Group Normalization 主要用于图像领域，对于一个 2-D 图像，它的 Tensor 是 4-D 的，即 (B, C, H, W)，Group Normalization 将 channels 分为几个 group，然后每个 group 内的所有元素做 normalization。这个操作只在单个样本上进行，不涉及 batch，所以可以用于一些 batch 比较小的场合。如果设置 group 为 1，那么 Group Normalization 就是 Layer Normalization。

Group Normalization 中的 scale and shift 是给每个通道一个参数，二者的形状是 $(C,)$

计算方差（或标准差）同样是有偏的

下面是一个 4-D Tensor with shape $(B, C, H, W)$ 计算均值和标准差的示意图，分成 $G$ 个 group，reshape 成 $(B, G, C/G, H, W)$计算得到的均值和方差的形状是 $(B, G)$，再广播成 $(B, G, C/G, H, W)$ 的形状进行计算，最后再 reshape 成输入的形状。

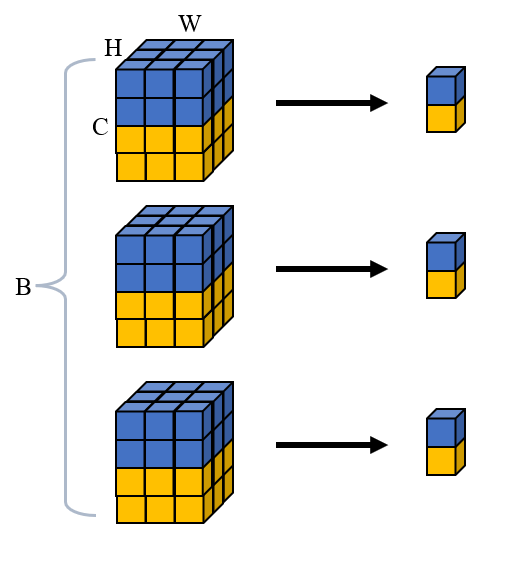
计算过程不好用公式表示，这里直接用代码：

# x shape=(B, C, H, W)
x_shape = x.shape
x = x.view(batch_size, groups, -1)  # shape=(B, G, C/G * H * W) 
x_mean = x.mean(dim=[-1], keep_dim=True)  # shape=(B, G, 1)
x_std = x.std(dim=[-1], keep_dim=True)  # shape=(B, G, 1)

x_norm = (x - x_mean) / (x_std + eps)  # shape=(B, G, C/G * H * W) 

y = x_norm.view(x_shape)

PyTorch 中的 torch.nn.GroupNorm 如下：

torch.nn.GroupNorm(num_groups, 
                   num_channels, 
                   eps=1e-05, 
                   affine=True, 
                   device=None, dtype=None)

这些参数没什么好讲的，见词知义，唯一需要强调一下的是 affine，涉及到 scale and shift，这两个可学习参数的是逐通道的，初始化如下：

1
2
3

if self.affine:
	self.scale = nn.Parameter(torch.ones(channels))
	self.shift = nn.Parameter(torch.zeros(channels))

自己实现简单的代码验证一下：

import torch
import torch.nn as nn

x = torch.randn(3, 8, 5, 5)

y_gn = nn.GroupNorm(num_groups=4, num_channels=8, affine=False)(x)# shape=(3, 8, 5, 5)

x_shape = x.shape
x = x.view(3, 4, 2, 5, 5)

x_mean = torch.mean(x, dim=(2, 3, 4), keepdim=True)  # shape=(3, 4, 1, 1, 1)
x_std = torch.std(x, dim=(2, 3, 4), unbiased=False, keepdim=True)  # shape=(3, 4, 1, 1, 1)
eps=1e-5
y_verify = (x - x_mean) / (x_std + eps)  # shape=(3, 4, 2, 5, 5)
y_verify = y_verify.view(x_shape)  # shape=(3, 8, 5, 5)

print(torch.sum((y_gn - y_verify) < 1e-4).item())

"""
outputs:
600
"""

4. 参考资料

labml.ai 的代码实现
PyTorch 文档

更新记录：

2022-4-9：第一版上传